Design of photonic integrated circuit

Design of photonic integrated circuit

Photonic integrated circuits (PIC) are often designed with the help of mathematical scripts because of the importance of path length in interferometers or other applications that are sensitive to path length. PIC is manufactured by pattering multiple layers (typically 10 to 30) on a wafer, which are composed of many polygonal shapes, often represented in the GDSII format. Before sending the file to the photomask manufacturer, it is strongly desirable to be able to simulate the PIC to verify the correctness of the design. The simulation is divided into multiple levels: the lowest level is the three-dimensional electromagnetic (EM) simulation, where the simulation is performed at the sub-wavelength level, although the interactions between atoms in the material are handled at the macroscopic scale. Typical methods include three-dimensional finite-difference Time-domain (3D FDTD) and eigenmode expansion (EME). These methods are the most accurate, but are impractical for the entire PIC simulation time. The next level is 2.5-dimensional EM simulation, such as finite-difference beam propagation (FD-BPM). These methods are much faster, but sacrifice some accuracy and can only handle paraxial propagation and cannot be used to simulate resonators, for example. The next level is 2D EM simulation, such as 2D FDTD and 2D BPM. These are also faster, but have limited functionality, such as they cannot simulate polarization rotators. A further level is transmission and/or scattering matrix simulation. Each major component is reduced to a component with input and output, and the connected waveguide is reduced to a phase shift and attenuation element. These simulations are extremely fast. The output signal is obtained by multiplying the transmission matrix by the input signal. The scattering matrix (whose elements are called S-parameters) multiplies the input and output signals on one side to find the input and output signals on the other side of the component. Basically, the scattering matrix contains the reflection inside the element. The scattering matrix is usually twice as large as the transmission matrix in each dimension. In summary, from 3D EM to transmission/scattering matrix simulation, each layer of simulation presents a trade-off between speed and accuracy, and designers choose the right level of simulation for their specific needs to optimize the design validation process.

However, relying on electromagnetic simulation of certain elements and using a scattering/transfer matrix to simulate the entire PIC does not guarantee a completely correct design in front of the flow plate. For example, miscalculated path lengths, multimode waveguides that fail to effectively suppress high-order modes, or two waveguides that are too close to each other leading to unexpected coupling problems are likely to go undetected during simulation. Therefore, although advanced simulation tools provide powerful design validation capabilities, it still requires a high degree of vigilance and careful inspection by the designer, combined with practical experience and technical knowledge, to ensure the accuracy and reliability of the design and reduce the risk of the flow sheet.

A technique called sparse FDTD allows 3D and 2D FDTD simulations to be performed directly on a complete PIC design to validate the design. Although it is difficult for any electromagnetic simulation tool to simulate a very large scale PIC, the sparse FDTD is able to simulate a fairly large local area. In traditional 3D FDTD, the simulation begins by initializing the six components of the electromagnetic field within a specific quantized volume. As time progresses, the new field component in the volume is calculated, and so on. Each step requires a lot of calculation, so it takes a long time. In sparse 3D FDTD, instead of calculating at each step at each point of the volume, a list of field components is maintained that can theoretically correspond to an arbitrarily large volume and be calculated only for those components. At each time step, points adjacent to field components are added, while field components below a certain power threshold are dropped. For some structures, this computation can be several orders of magnitude faster than traditional 3D FDTD. However, sparse FDTDS do not perform well when dealing with dispersive structures because this time field spreads too much, resulting in lists that are too long and difficult to manage. Figure 1 shows an example screenshot of a 3D FDTD simulation similar to a polarization beam splitter (PBS).

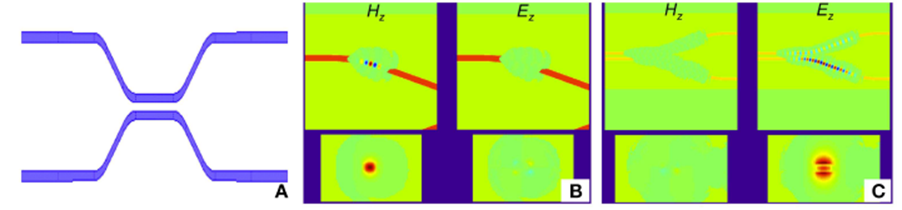
Figure 1: Simulation results from 3D sparse FDTD. (A) is a top view of the structure being simulated, which is a directional coupler. (B) Shows a screenshot of a simulation using quasi-TE excitation. The two diagrams above show the top view of the quasi-TE and quasi-TM signals, and the two diagrams below show the corresponding cross-sectional view. (C) Shows a screenshot of a simulation using quasi-TM excitation.